【電験三種】直流機の誘導起電力の式（e=pφNZ/60a）の導出

2024年8月24日 2024年8月24日

NORI

今回は電験三種機械科目の「直流機」に登場する以下の式、

$$e=\frac{N}{60}pφ\frac{z}{a}[V]$$

の導出について解説していきたいと思います。

導出

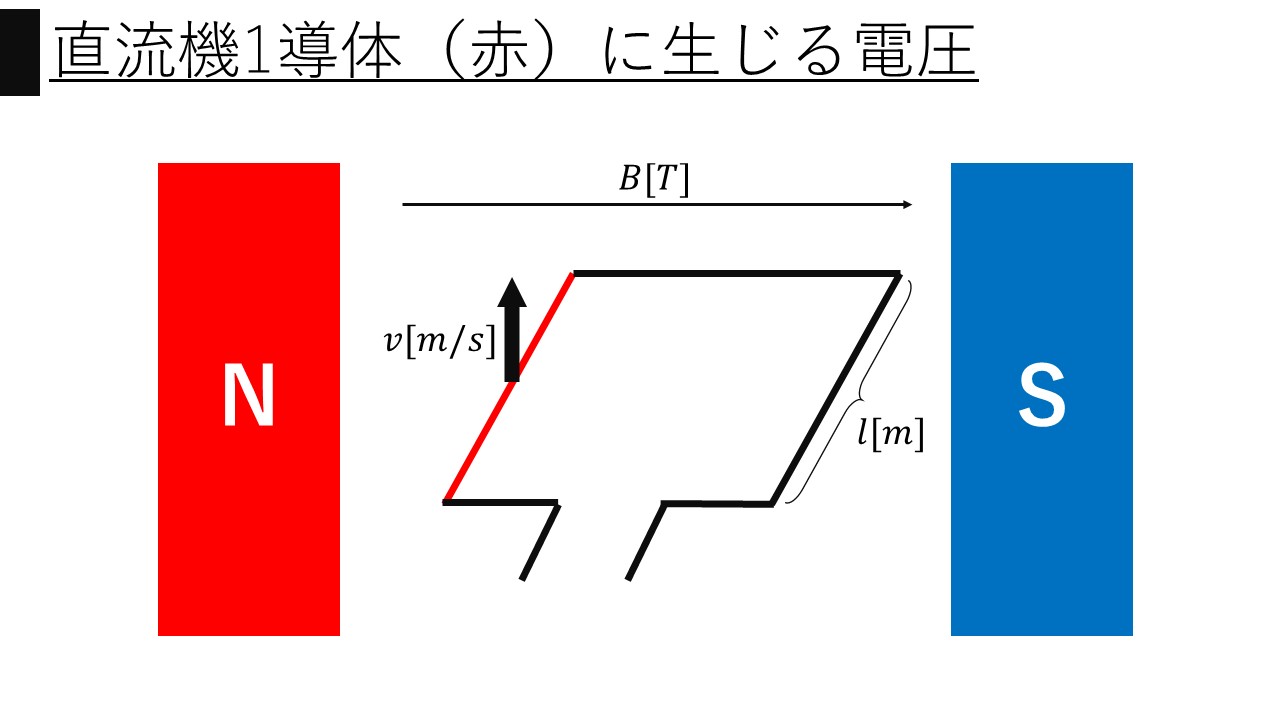
まずは＜画像1＞中に示した１コイルのコイル辺に生じる起電力$e_{1}$は以下の式で表されるのでした。

$$e_{1}=vBl[V]$$

ただし、$v[m/s]$は周速度、$B[T]$は磁束密度、$l[m]$はコイル辺の長さ

ここから$v[m/s]$と$B[T]$を＜画像2＞のように、直径$D[m]$、回転速度$N[min^{-1}]$、一極当たりの磁束$φ[Wb]$を用いて表していきます。

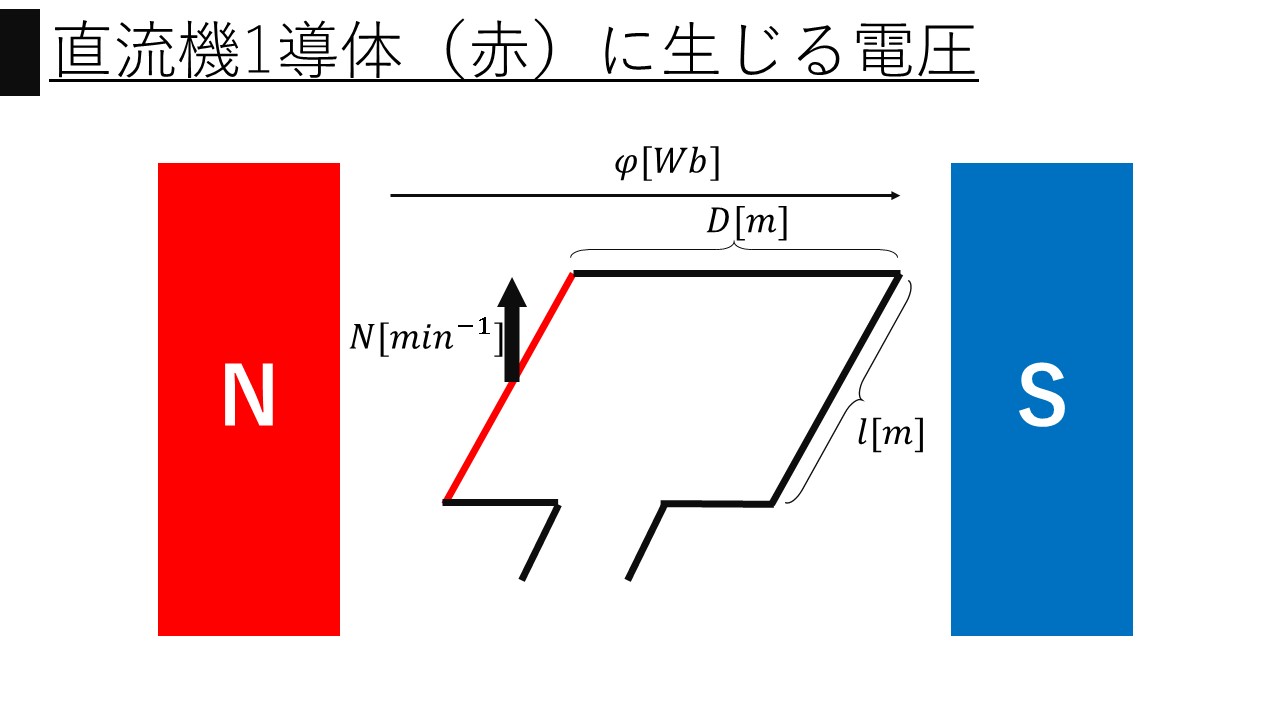
ではまずは、周速度$v[m/s]$を回転速度$N[min^{-1}]$を用いて表していきます。

回転速度$N[min^{-1}]$は”一分間にN回転する”という意味なので、これを秒単位に変換すると、$\frac{N}{60}[s^{-1}]$となります。次に一回転の長さ（円周）を求めると、$πD[m]$となります。ということで、周速度$v[m/s]$は、

$$v=\frac{πDN}{60}[m/s]$$

となります。

次に磁束密度$B[T]$を極数$p$と一極当たりの磁束$φ[Wb]$を用いて表します。磁束密度の単位は$[Wb/m^{2}]$とも表されます。これは磁束を回転子表面積で割ってあげた単位になります。

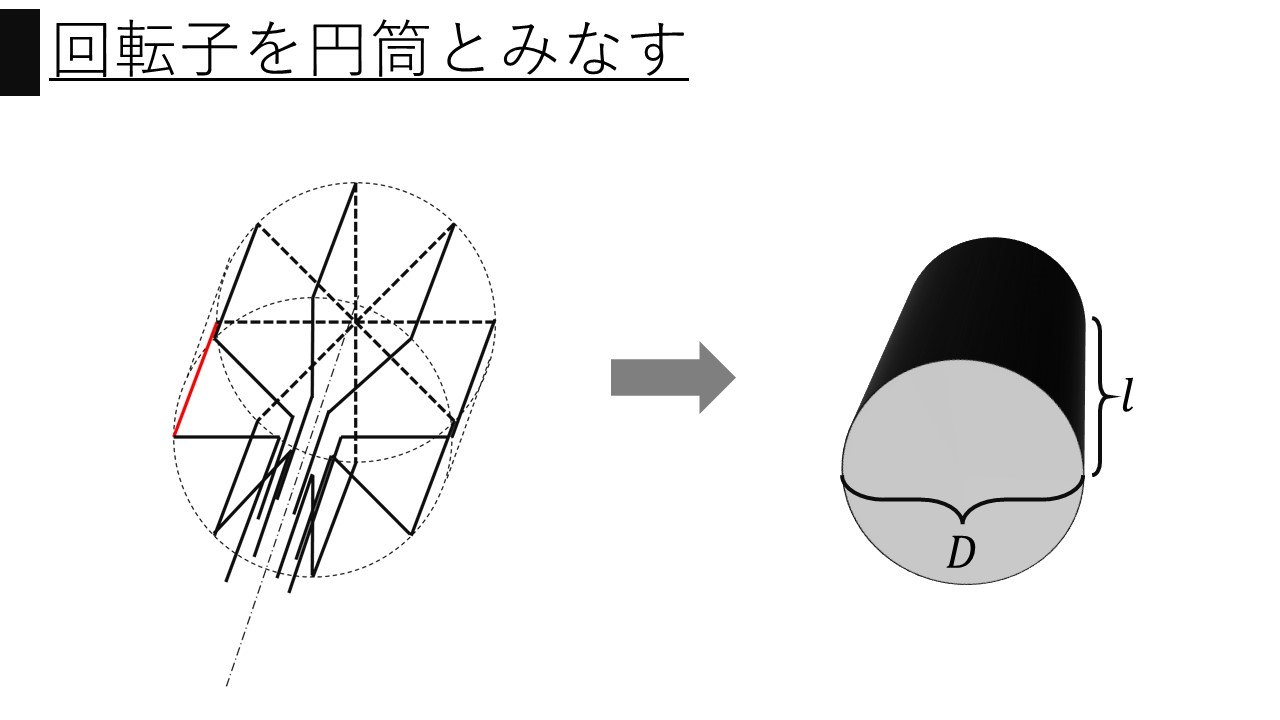
＜図3＞のように回転子を円筒とみなすと、側面（黒色の部分）の表面積$S$は、$$S=πDl[m^{2}]$$となります。全磁束$Φ[Wb]$は、磁極数$p$と、一極当たりの磁束$φ[Wb]$を用いて、$$Φ＝pφ[Wb]$$となり、磁束密度$B[Wb/m^{2}]$は、

$$\begin{align}B&=\frac{Φ}{S}\\&=\frac{pφ}{πDl}[Wb/m^{2}]\end{align}$$

となります。ということで、コイル辺に生じる起電力の式に代入すると、

$$\begin{align}e_{1}&=vBl\\&=\frac{πDN}{60}×\frac{pφ}{πDl}×l\\&=\frac{N}{60}pφ[V]\end{align}$$

となりました。これは”1導体”に生じる起電力の式であるので、これを”1直列回路”に生じる起電力の式に直します。よく電験の問題文には「全導体数を$z$とし、並列回路数を$a$とする」とありますが、これは＜画像4＞に示すようなイメージになります。

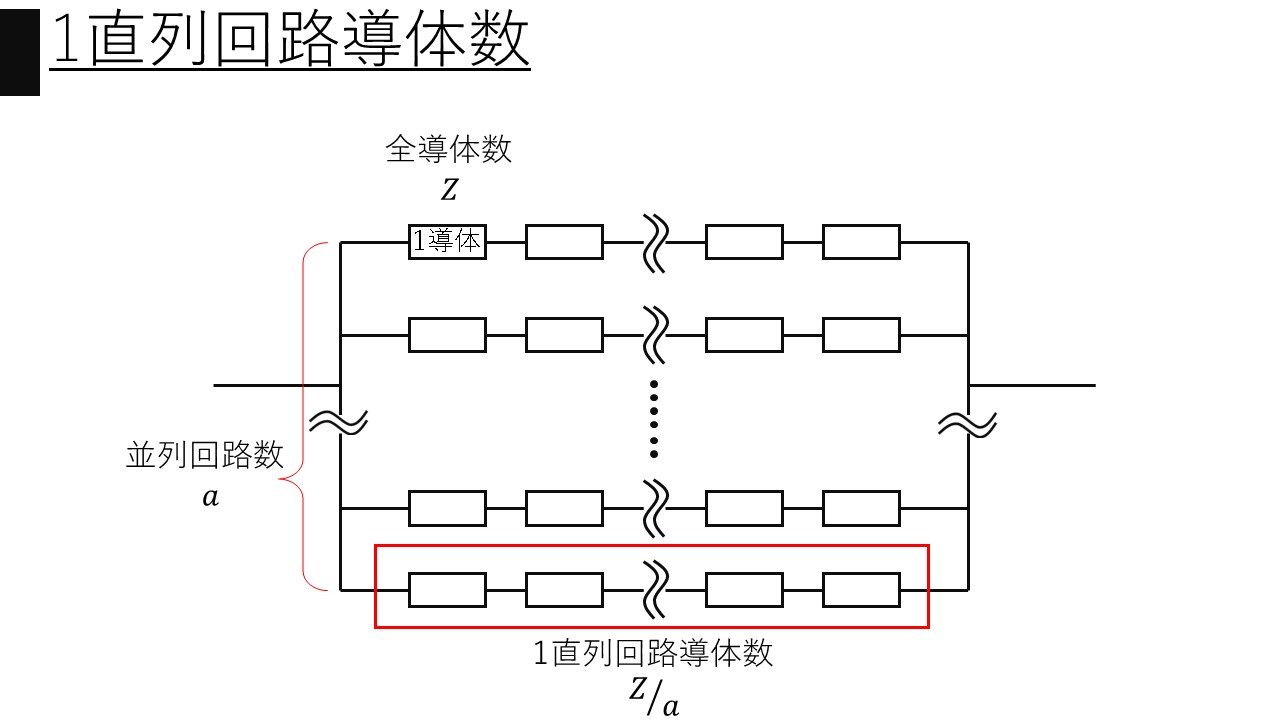
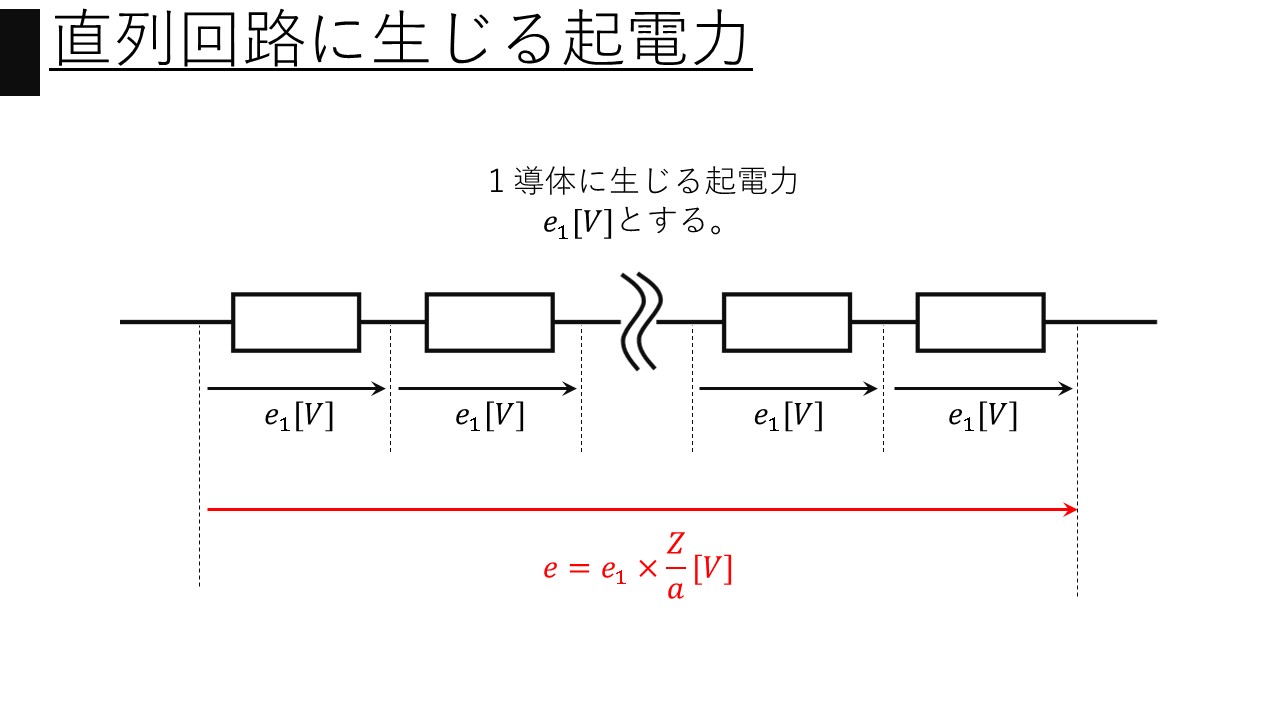
＜画像5＞より、”1直列回路”に生じる起電力$e$は、

$$\begin{align}e&=e_{1}×\frac{Z}{a}\\&=\frac{N}{60}pφ\frac{Z}{a}\end{align}$$

となり、導出終了です。

過去問で使ってみる

＜H27年度（2015年）問1＞

4極の直流電動機が電機子電流250A、回転速度$1200min^{-1}$で一定の出力で運転されている。電機子導体は波巻であり、全導体数が258、１極当たりの磁束が0.020Wbであるとき、この電動機の出力の値[kW]として、最も近いものを次の（１）～（５）のうちから一つ選べ。
ただし、波巻の並列回路数は2である。また、ブラシによる電圧降下は無視できるものとする。

（１）8.21　（２）12.9　（３）27.5　（４）51.6　（５）55.0解答を見る（４）